Simple cryptography for the rest of us | Just Reflections - Issue #25
This is part 3 of a series on cryptocurrencies. If this is your first time here, I highly advise that you start with parts one and two:
Last week we closed with a question.
If anyone can have a ledger and a transaction happens at any ledger and is then broadcast to the rest of the ledgers, what stops me from creating a transaction pretending to be someone else, sending their money to my account and then broadcasting that transaction to the network of ledgers?
Now that our fantasy town has developed People Coin to decentralise from the potentially untrustworthy village chief, they need ways of maintaining the monetary system without a central authority to check everything. In particular, they need some way to verify that a transaction is valid and to prove their personal identities.
I’ve mentioned a few times in this series that cryptocurrencies use mathematics and algorithms to achieve security. I’ve done my best to explain everything else without getting into how that works, but we can’t avoid it any longer. Fortunately, a couple of years ago, I read a brilliant series of articles on cryptography — which completely went over my head at the time because it was not relevant. But now that I had a good reason, I went back to it and today, I will attempt to give a high-level overview of cryptography by summarizing that series in a way that the rest of us can understand. It’s a big feat, so let’s jump in.
Asymmetric Encryption
Cryptocurrencies use what is called public-key cryptography or asymmetric encryption. In order to explain what that is, we need to go through a few core concepts. Here’s the roadmap for today:
Hashing
Message Integrity
Confidentiality
Symmetric Encryption
Asymmetric Encryption
Hashing
The first concept in our exploration is that of a hashing algorithm. But before we go far, I need to define what an algorithm is. The Oxford dictionary actually has a brilliant definition:
A process or set of rules to be followed in calculations or other problem-solving operations, especially by a computer. — Definitions from Oxford Languages
An algorithm, in its simplest terms, is a set of instructions for doing a task. By this definition, you would think that a recipe for baking a cake is the “cake making algorithm” and you’d be correct to think that.
Now, what is hashing?
Hashing is converting a message into another — usually simpler — representation of itself. A simple example of hashing is if I take a word and assign numbers to its letters according to their position in the alphabet and then add them to create a number that represents the word:
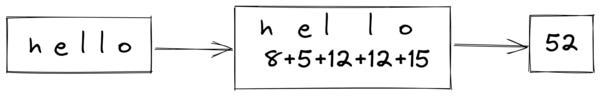
In the image above, we have hashed the word hello into the number 52. The hashing algorithm is the set of instructions for how we achieve this, that is;
Change each letter to a number according to its position on the alphabet
Add up the numbers
The result is the hash that represents that word.
That’s it, that’s a basic hashing algorithm.
The result of a hashing algorithm is called a Digest (or sometimes a Checksum or Fingerprint). If someone were to change the message and take it through the hashing algorithm again, the digest would also change. For example:
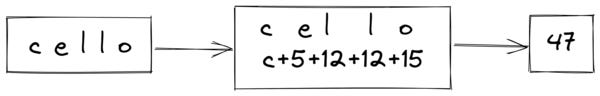
By comparing message digests, we can determine that the message has changed.
Note that our current hashing example is not perfect in showing us when our message changes. There are many words that can produce the same digest. cellt for example, would also produce a digest of 52. In reality, a hashing function must have the following four qualities to be used in cryptography:
It should be mathematically impossible to extract the original message from the digest
A slight change in the original message should cause a drastic change in the digest
The digest should always be the same length regardless of the length of the message
It is not feasible to construct a message which generates a given digest.
Because of this, hashing is sometimes referred to as one-way encryption. The message can be encrypted but is impossible to decrypt it.
Message Integrity
In the world of secured communications, Message Integrity describes the concept of ensuring that data has not been changed in transit. We can achieve this with hashing algorithms (remember, we said once a message is encrypted, it can’t be decrypted).
Imagine you want to send a message to your friend and you want to ensure that the message is not changed while in transit. You would calculate the hash of the message and send the digest together with the message. When your friend receives it, they also hash the message and compare the digests. If they are the same, then the message has not been tampered with.
Pretty straight forward right?
Well, there’s a problem. If someone intercepted the message, changed it, and recalculated the digest before sending it along its way, your friend’s hash calculation would also match the changed message.
So how do we fix this?
By adding a secret key, known only by you and your friend, to the message before calculating the digest. This way, someone who intercepts the message would not know what secret key to add to create the correct digest. So when your friend receives the message, adds the secret and calculates a matching hash, they can be sure that:
the message was definitely not altered in transit
the message was definitely sent by someone with the secret key, hopefully, you.
Of course, there is still an important question to ask. How did the sender and receiver share the secret key in the first place? This is known as the Key Exchange Problem. It comes up a few times in cryptography. We will look at how to solve it later.
Confidentiality
In cryptography, confidentiality is the concept of hiding or scrambling your data so that only the intended recipient has access. This is typically accomplished by some means of Encryption. The major difference between hashing and encrypting is that encryption can be reversed and hashing cannot.
Data, before it has been encrypted, is referred to as plaintext, or clear text. After the data has been encrypted, it is referred to as ciphertext. The process by which the plaintext is converted to ciphertext is known as the encryption algorithm. Remember, an algorithm is just a set of instructions for doing a particular thing. The “thing” in this case is hiding your message. Modern confidentiality uses what is sometimes referred to as cryptographic encryption. Which is combining a publicly known encryption algorithm along with a secret key similar to what we saw in the hashing example.
There are two types of cryptographic encryption: Symmetric Encryption and Asymmetric Encryption. The major difference between the two is that symmetric encryption uses the same key to encrypt and decrypt the message and asymmetric encryption uses two different keys.
Symmetric Encryption

In the image above, we use symmetric encryption to encrypt the message hello using a secret key of 3 and we end up with a ciphertext of khoor. Our algorithm is shifting each letter forward in the alphabet by the number of times given in the secret key. To decrypt, you need to know this encryption algorithm, then you can apply it in reverse and get the message in plain text.
We can illustrate this with some simple math as well. For example, if we have plaintext of 11 we can use the symmetric encryption algorithm of multiplication along with a secret key 5 to get 11 x 5 = 55. To decrypt our ciphertext, we reverse the algorithm (by using division) and apply the same secret key of 5 to get 55 ÷ 5 = 11.
One of the major drawbacks of symmetric encryption is that the secret key used to encrypt and decrypt must exist in two different locations. The key exchange problem again, how do we get the key securely from one party to the other? Even if we do find a way to share the key, its security is at the mercy of the weakest link. If the party you are in communication with lacks basic security best practices, that puts your key (and therefore your data) at risk. This leads us nicely to asymmetric encryption.
Asymmetric Encryption

In the example above, we use the same encryption algorithm we used for symmetric encryption to take the plaintext hello, encrypt it with the secret key 5 and get ciphertext mjqqt. However, for decryption instead of simply reversing the encryption, we continue moving the letters forward 21 more times to get the original message:

Of course, in this simplistic example, we could have simply moved backwards in the alphabet with the encryption key of 5 and gotten the message. But in a real asymmetric encryption algorithm, attempting to re-use the encryption key would simply scramble the text further.
That said, the example is still able to illustrate an important point. We used an encryption key 5, and could decrypt successfully with a decryption key of 21. But we could also have used an encryption key of 21, and successfully decrypted it with a decryption key of 5. The asymmetric keys are mathematically linked. What one key encrypts, only the other can decrypt — and vice versa.
So what can we do with an asymmetric key pair? One of these keys can be stored securely and never shared with anyone. This key is called the Private Key. The other key is called the Public Key and is made available to the world. Every participant in asymmetric encryption has their own unique key pair. Then each of these keys can be used in different ways in order to get unique security features.
The primary (and most significant) benefit to using asymmetric encryption is the private key never needs to be shared, hence solving the key exchange problem. There is no risk of compromise while the key is being transferred (since it never needs to be transferred at all). There is no risk of compromise from the other party’s potential lack of security (since the other party never has your private key).
Cryptocurrencies
Below is an illustration of Bob (on the right in red) and Alice (on the left in purple). Since Bob and Alice are two unique entities, they each have their own set of public and private keys. Their public keys are on the inside, available to each other. While their private keys are on the outside, hidden and out of reach.

Let’s imagine that Alice wants to send a message to Bob. Alice is very concerned that Bob knows beyond any doubt that it was definitely Alice that sent the message.
Alice can use her private key to encrypt the message. Which makes it so the only key in the world that can decrypt her message is her public key — which she knows Bob (and anyone else) has access to. The message is sent to Bob, who then uses Alice’s public key to decrypt the message. If Bob was able to successfully extract the message, then he can be assured that the message must have been originally encrypted by Alice’s Private Key. And since Alice never shared her Private Key with anyone, Bob can be assured that Alice indeed sent the message and that the message has not been tampered with in transit.
This process is known as Message Signing. It is a creative use of the fact that asymmetric keys are mathematically linked, and that what one key encrypts, only the other can decrypt.
So what does all this have to do with cryptocurrencies and money?
When you make a transaction with money (in whatever form) there are several assurances you need from the monetary system. Among them is that you need to be sure that when you make a transaction, no one can alter it in transit and defraud you of your money. And the people receiving the transaction need to be sure that it’s indeed you who sent that transaction. Therefore, you need to sign the transaction and message signing provides exactly this feature to cryptocurrencies.
When you create a cryptocurrency wallet, you get two asymmetric keys. Whenever you make a transaction, it will be signed with your private key as an assurance of its origin and to ensure its integrity and your public key can verify this. This is exactly what was missing from our cryptocurrency People Coin.
So what stops me from creating a transaction, pretending to be someone else, sending their money to my account and then broadcasting that transaction to the network of ledgers? It’s me not having their private key. So even if I can fake all the details, I have no way of signing the transaction so that it will be verified by the person’s private key.
With this new system of asymmetric encryption, People Coin can be divorced from any central authority and can be open to everyone.
Asymmetric encryption gives People Coin three key features:
Everyone has an identity that no one else can fake.
Everyone can sign transactions.
Everyone can verify that transactions are valid.
With that, we’ve come to the end of our series on cryptocurrencies. I know there’s a lot we didn’t cover, but I hope this has been enough to whet your appetite to discover more on your own. What did you think of this series? Would you like to see more of this type of writing in the future? I’d love to hear your thoughts, so please hit reply and let me know.
That’s all I have for you this week. If you like the newsletter, consider sharing it with others on Twitter, WhatsApp or Facebook. Hit the thumbs up or thumbs down below to let me know what you think.
I hope I’ve given you something to think about this week and I wish you ever-increasing curiosity.
Until next week.
BK
Impactful ideas that challenged my thinking.
I have a lot of interests so I'm always learning all kinds of things, some of which really challenge my thinking. In the Just Reflections newsletter, I'll be sharing with you a summary of the ideas that challenged my thinking recently and hopefully they will challenge yours too and we grow together.
In order to unsubscribe, click here.
If you were forwarded this newsletter and you like it, you can subscribe here.
Powered by Revue


