The Prisoner's Dilemma | Just Reflections - Issue #37

When going through normal life in casual situations, you probably aren’t thinking about mathematics all the time. But there’s an entire field of math and science that applies specifically to social interactions that I think we can all learn a lot from. It’s called “Game Theory”.
The prisoner’s dilemma
Consider this thought experiment.
You, let’s call you Thabo, and your friend, Musa, have just been arrested for some minor crime. The police believe you’ve committed a much bigger crime but they don’t have enough evidence to convict you. To try and force a confession the police lock you in different interrogation rooms and lay out the consequences to each of you.
Both you and Musa will get 10 years in prison each if both of you confess to the big crime and dish out dirt about each other. If one of you confesses and the other doesn’t, the one who confessed gets immunity and will go free and the one who didn’t will spend 20 years in prison. You both know that the police don’t have any evidence and If neither of you confesses, you each get 5 years for the minor crime.
Let’s show this in a picture:
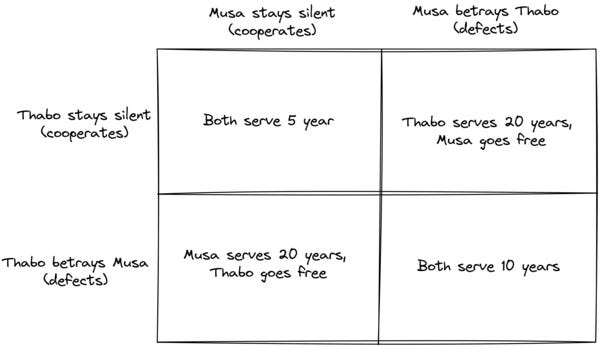
You can’t speak to each other and don’t know what the other person has decided. You’re friends, yes, but neither of you has any special loyalties towards one another, so you have no reason to think that Musa wants to protect you. Both of you are criminals, after all. What do you do?
This is called “The prisoner’s dilemma”.
Game Theory
Game theory was put into the mainstream in the 1950s by a mathematician called John Nash. This is the character that Russell Crow was playing in “A beautiful mind”. But game theory isn’t about games in how we normally think about them. Instead, a game is;
Any interaction between multiple people in which each person’s payoff is affected by the decisions made by others.
Sure this applies to games like chess and poker. But it also applies to any situation where people get together and interact. If you have interacted with anyone today, you can probably analyze all the decisions you made using game theory. It’s incredibly wide-ranging and is used all the time by economists, political scientists, biologists, military strategists and psychologists, just to name a few.
Game theory has two main branches; cooperative and non-cooperative. Non-cooperative game theory has to do with competitive social interactions where there will be some winners and some losers. It’s often referred two as a zero-sum game, the winning of one side necessarily means the losing of another and vice-versa. The prisoner’s dilemma falls into this category.
Then there are cooperative games where each player has agreed to work together towards a common goal. This could be anything from a group of friends deciding how to split the cost of a road trip to a coalition of nations deciding how to divide the burden of solving climate change.
In game theory, a coalition is a group of players in a cooperative game. The primary question in cooperative games is how much each player should contribute to the coalition and how much they should benefit from it. It tries to determine what’s fair. It achieves this by applying these precepts;
The contribution of each player is determined by what is gained or lost by removing them from the game. This is called their marginal contribution. If on our road trip you’re the only one with a car, your marginal contribution is a car, that’s what we lose by removing you from the coalition.
Interchangeable players have equal value. If two parties bring the same things to the coalition, they should have to contribute the same amount and should be rewarded for their contribution equally.
Dummy players have zero value. If a member of the coalition contributes nothing then they should receive nothing.
If a game has multiple parts, cost or payment should be decomposed across those parts.
We’ll look at cooperative games another day, for now, let’s go back to the prisoner’s dilemma.
The dominant strategy
The prisoner’s dilemma contains all elements of a game. The two players are Thabo and Musa. There are two strategies available to them, confess or don’t confess and the payoff of the game range from going free to serving either 5, 10 or 20 years in prison. Moves are simultaneous, which means neither player knows the other player’s decisions and decisions are made at the same time.
Both prisoners are in separate rooms and won’t be let out until both have made their decisions. One common solution to simultaneous games is called the dominant strategy. This is defined as the strategy that has the best payoff, regardless of what the other player chooses.
You don’t know if Musa will confess or not so you consider your options. If Musa doesn’t confess then you’re better off confessing because that way you would go free.

If Musa confesses, you’re better off if you also confessed otherwise you’ll get 20 years instead of 10.

Regardless of what Musa decides, your best option is to confess because it leads to the best payoff either way. Confessing means you either go free or serve less prison time than if you don’t confess.
When all players choose the dominant strategy, they reach what is called Nash equilibrium in game theory, named after John Nash.
The players in a game has found Nash equilibrium when they all make the choice that leaves them better off no matter what their opponents decide to do.
The prison’s dilemma is just one example of a competitive game but the basic idea behind its solution applies to all sorts of situations. Generally;
When you’re competing with others, it makes sense to choose the course of action that benefits you the most no matter what everyone else decides to do.
Ideally, you should have both stayed silent then you both get 5 years which is less than both the 10 years and then 20 years. But that is an unstable state because you have no way of ascertaining that Musa will also confess. From an individual standpoint, the best course of action is to confess if you have no control over what the other person will do.
The best option becomes to confess to better your own situation, which effectually hurts both the group, which could have gotten 5 years each and yourself. The guys at Crash Course Economics give a brilliant explanation of how game theory applies to real-world economics.

Game Theory and Oligopoly: Crash Course Economics #26
When playing competitive games in the real world things are a little different and you can alter some variables to bend the odds. For example, the situation assumes the players can only play once. But the game changes if the players have a chance to build a relationship and work together to get more gains over time or punish each other by not cooperating. Naval Ravikant explains this really well.

Naval Ravikant: The Prisoner's Dilemma
The prisoner’s dilemma and similar games illustrate how rationality can be problematic in game theory. The issue here is that the theories rely on the assumption that agents are rational players who strive to maximise their utility and payoff. But the conclusions of rational analysis fail to conform to reality because people don’t always act rationally. There’s more to real people. Even in one-off scenarios with no guarantees or obligations and no chance to build a relationship, we’re still concerned about how the group might decide. In real-world studies that ran the prisoner’s dilemma with real people, they didn’t confess over 20% of the time.
Competitive interactions can get much more complicated than the prisoner’s dilemma and there’s a lot more to game theory. But the fundamental point of value is that in a competitive situation, game theory can teach you how to be smart. So it’s definitely worth spending some time understanding it.
If this stuff interests you, check out this game show called Golden Balls which pays on the prisoner’s dilemma.

golden balls. the weirdest split or steal ever!
And if you’re looking for something a bit more serious, here’s Matt Ridley and Jordan Peterson discussing the prisoner’s dilemma.

The Prisoner's Dilemma Game | Matt Ridley & Jordan B. Peterson
That’s all I have for you this week. If you like the newsletter, consider sharing it with others on Twitter, WhatsApp or Facebook. Hit the thumbs up or thumbs down below to let me know what you think.
I hope I’ve given you something to think about this week and I wish you ever-increasing curiosity.
Until next week.
BK
2022 Resolutions:
Weight: Get to 75kg by April 28 and 70kg by July
This chart is worryingly starting to trend in the wrong direction. I can explain myself though. I have several projects running in parallel and I’m working almost totally round the clock, this means I’m getting very little exercise since most of my day I’m hunched at my desk. I can’t wait to get a bit more time to do other things.

Sleep: Consistently sleep avg. 8 hours per day
Averages this week:
Duration: 7h 23m.
Avg. bedtime: 01:48.
Avg. wake-up time: 08:33.
I didn’t include this one last week coz the numbers were horrible and I was frankly a little discouraged. Thankfully, jetlag was hitting me hard this week and by 7 - 8 pm I was just finished. I was trying to push myself since I had so much to do but I was out just after midnight on most days.
Business: Start a business in 2022
I’ve been working on a secret project for the last three months and I’m happy to finally announce that in 2 week’s time, we’ll be launching dealbase.africa, an exciting platform to showcase Africa’s fundraising success, equip founders to raise capital and enable investors to optimise deal flow. Follow dealbase.africa on LinkedIn for more.
Impactful ideas that challenged my thinking.
I have a lot of interests so I'm always learning all kinds of things, some of which really challenge my thinking. In the Just Reflections newsletter, I'll be sharing with you a summary of the ideas that challenged my thinking recently and hopefully they will challenge yours too and we grow together.
In order to unsubscribe, click here.
If you were forwarded this newsletter and you like it, you can subscribe here.
Powered by Revue

